Quadratic on a Sphere
Another problem naturally leading to a different secular equation is finding stationary values of a quadratic function defined by on the unit sphere . This was first studied by Forsythe and Golub [1965]. Their treatment was subsequently simplified and extended by Spjøtvoll [1972] and Gander [1981]. The problem has recently received some attention because of the development of trust region methods for optimization, and, indeed, because of Nesterov majorization.
The stationary equations are Suppose with the , change variables to , and define . Then we must solve Assume for now that the elements of are non-zero. Then cannot be equal to one of the . Thus and we must have , where Again, let's look at an example of a particular . The plots in Figure 1 show both ad . We see that has 12 solutions, so the remaining question is which one corresponds with the minimum of .
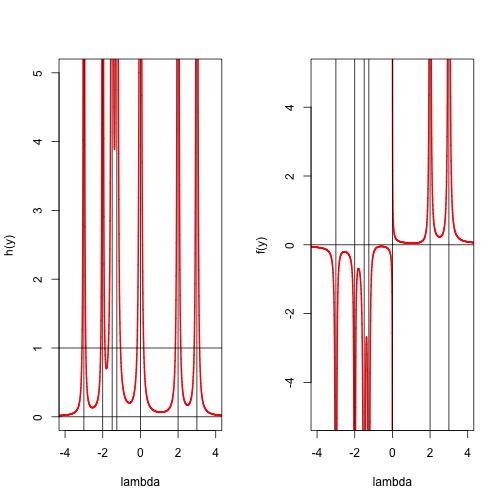
Again has vertical asympotes at the . Beween two asymptotes decreases from to a minimum, and then increases again to . Note that and and thus is convex in each of the intervals between asymptotes. Also is convex and increasing from zero to on and convex and decreasing from to zero on .