I.4.3.1: The Cartesian Folium

The ``folium cartesii'' (letter of Descartes to Mersenne, August 23, 1638) is the function $f:\mathbb{R}^2\rightarrow\mathbb{R}$ defined by $$f(x,y)=x^3+y^3-3xy.$$

The gradient is $$\mathcal{D}f(x,y)=\begin{bmatrix}3x^2-3y\\3y^2-3x\end{bmatrix},$$ and the Hessian is $$\mathcal{D}^2f(x,y)=\begin{bmatrix}6x&-3\\-3&6y\end{bmatrix}.$$ It follows that $f(x,y)$ has a saddle point at $(0,0)$ and an isolated local minimum at $(1,1)$. These are the only two stationary points. At $(0,0)$ the eigenvalues of the Hessian are $+3$ and $-3$, at $(1,1)$ they are $9$ and $3$.

The Hessian is singular if and only if $(x,y)$ is on the hyperbola $xy=\frac14$. It is positive definite if and only if $(x,y)$ is above the branch of the hyperbola in the positive orthant.

See Figure 1 for contour plots of sections of $f$ on two different scales.

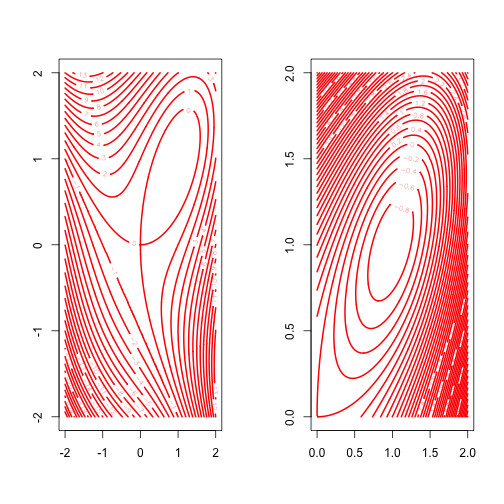
Now apply coordinate descent [De Leeuw, 2007b]. The minimum over $x$ for fixed $y$ only exists if $y>0$, in which case it is attained at $\sqrt{y}$. In the same way, the minimum over $y$ for fixed $x>0$ is attained at $\sqrt{x}$. Thus the algorithm is simply $$\begin{align*} x^{(k+1)}&=\sqrt{y^{(k)}},\\ y^{(k+1)}&=\sqrt{x^{(k+1)}}, \end{align*}$$ and the algorithmic map is $$\mathcal{A}(x,y)=\begin{bmatrix}\sqrt{y}\\\sqrt[4]{y}\end{bmatrix}.$$ The algorithm can only work if we start with $y^{(0)}>0$. It then converges, linearly and monotonically, to $(1,1)$ with convergence rate $\frac14$. If we start with $y^{(0)}\leq 0$ then $x^3+(y^{(0)})^3-3xy^{(0)}$ is unbounded below and thus coordinate descent fails.