I.4.3.4: Rayleigh Quotient
The problem is to minimize the Rayleigh quotient over all Here and are known matrices, with positive definite.
If we update to with a unit vector, then Think of this as a continous rational function of the single variable , which we have to minimize. Clearly has a horizontal asymptote, with Also with and In addition and thus and at values where we have .
We now distinguish three cases.
- First, can be a constant function, everywhere equal to . This happens only if or , which makes for all . In this case we do not update, and just go to the next .
- Second, can have a zero quadratic term. If we make sure that then the unique solution of the linear equation satisfies , and consequently corresponds with the unique minimum of . Updating guarantees that we will have for all subsequent iterations. If we happen to start with or wind up in a point with a zero quadratic term and with then does not have a minimum and coordinate descent fails.
- If is a proper quadratic then is either increasing at both infinities or decreasing at both infinities. In the first case, when is a convex quadratic, increases from the horizontal asymptote to the maximum, then decreases to the minimum, and then increases again to the horizontal asymptote. In the second case, with a concave quadratic, decreases from the horizontal asymptote to the minimum, then increases to the maximum, and then decreases again to the horizontal asymptote. In either case it has two extremes, one minimum and one maximum, corresponding to the roots of the quadratic . This also shows that if is a proper quadratic, then it always has two distinct real roots.
Here is some simple code to illustrate the cases distinguished above. We have a simple function to compute .
Case 2, with the zero quadratic term, and Case 3, the proper quadratic, are illustrated with
a <- matrix (-1, 3, 3)
diag (a) <- 1
b <- diag (3)
x <- c(1, 1, -1)
zseq <- seq (-8, 8, length = 100)
png("myOne.png")
plot (zseq, fRayleigh (zseq, 1, x, a, b),type="l",cex=3,col="RED",xlab="theta",ylab="lambda")
abline(h=a[1,1] / b[1,1])
dev.off()
x <- c(1,0,1)
png("myTwo.png")
plot (zseq, fRayleigh (zseq, 2, x, a, b),type="l",cex=3,col="RED",xlab="theta",ylab="lambda")
abline(h=a[2,2] / b[2,2])
dev.off()
For Case 2 we see that has no minimum, and CCD fails. For Case 3, which is of course the usual case, there are no problems.
The coordinate descent method can obviously take sparseness into account, and it can easily be generalized to separable constraints on the elements of such as non-negativity. Note that it also can be used to maximize the Rayleigh quotient, simply by taking the other root of the quadratic. Or, alternatively, we can interchange and .
The second derivative of the Rayleigh quotient at a stationary point normalized by is simply This is singular and thus the product form of the derative of the algorithmic map has largest eigenvalue equal to one, corresponding with the eigenvector . Singularity of the Hessian is due, of course, to the fact that is homogenous of degree zero, and rescaling does not change the value of the objective function. We can use this to our advantage. Suppose we normalize to , after each coordinate descent cycle. This will not change the function values computed by the algorithm, but is changes the algorithmic map. The derivative of the modified map is which has the same eigenvalues and eigenvectors as , except for , while .
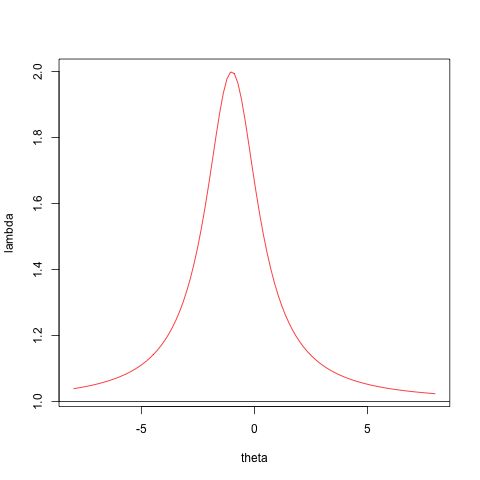
Figure 1: Case 2 -- CCA Fails </center>
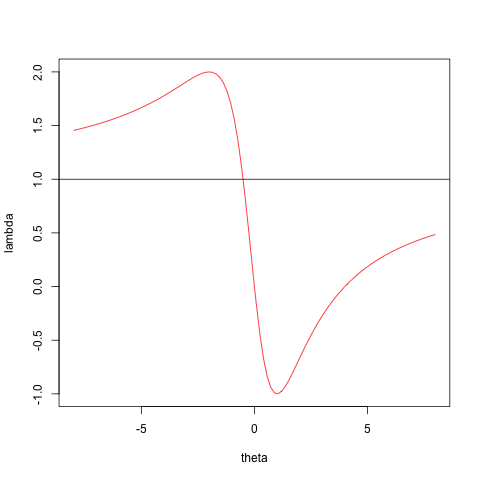
Figure 2: Case 2 -- CCA Works </center>