Logit
The logistic distribution increases from zero to one on the real line. As we have seen before, the function is strictly convex. This follows directly from because the first derivative is increasing and the second derivative is positive.
Theorem: The r-th derivative is a polynomial in of degree . Consequently for all there are two finite real numbers such that for all .
Proof: We know that , and thus the result is true for . Now proceed by induction. If for some polynomial of degree , then which is indeed a polynomial in of degree . In addition and the quantities on the right-hand side are clearly finite. QED
We illustrate the theorem by computing some higher derivatives which implies The derivatives of orders 2 to 5 are in Figure 1.
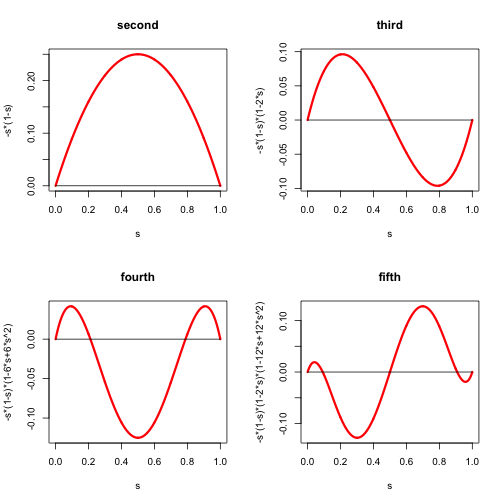
And here is some
R code for drawing the figure.
We now look more closely at the polynomials . From the proof of the we see that for we have . Because we see that actually for all even and for all odd . This implies that for all odd .
We can go further than this and derive an explicit formula for the polynomials. The difference/differential equation we have to solve is where . Its general solution is where the are the Stirling numbers of the second kind (the number of ways of partitioning elements into non-empty subsets).
The code in logitPom.R computes the polynomials . With logitPomRecursive(n) we compute all polynomials up to order n, their roots, and their maximum and minimum values. With logitPomDirect(n) we do the same, using the formula with Stirling numbers.
Maybe useful 03/02/15