Majorization at a Point | Block Relaxation Algorithms in Statistics -- Part II

II.1.2.1: Majorization at a Point

Suppose $\ f$ and $g$ are real-valued functions on $\mathcal{X}\subseteq\mathbb{R}^{n}$ . We say that $g$ majorizes $\ f$ over $\mathcal{X}$ at $y\in\mathcal{X}$ if

$g(x)\geq f(x)$ for all $x\in\mathcal{X}$ ,
$g(y)=f(y)$ .

If the first condition can be replaced by

$g(x)$ > $f(x)$ for all $x\in\mathcal{X}$ with $x\not= y$ ,

we say that majorization at $y\in\mathcal{X}$ is strict.

Equivalently majorization is strict if the second condition can be replaced by

$g(x)=f(x)$ if and only if $x=y$ .

Since we formulate all optimization problems we encounter as minimization problems, we only use majorization, not minorization. But just for completeness, if $g$ majorizes $f$ at $y$ over $\mathcal{X}$ , then $f$ minorizes $g$ at $y$ over $\mathcal{X}$ .

We will see plenty of examples as we go on, but for now a simple one suffices. Figure 1 shows the logarithm on $\mathbb{R}^+$ strictly majorized at $+1$ by the linear function $g:x\rightarrow x-1.$

Figure 1: Linear Majorizer of the Log at +1

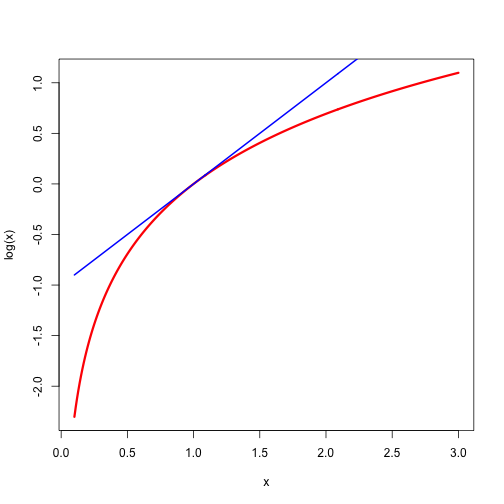
Note that the definition of majorization at a point always has to take the set $\mathcal{X}$ into account. If $g$ majorizes $f$ over $\mathcal{X}$ at $y$ , then it may very well not majorize over a larger set. But, of course, it does majorize $f$ at $y$ over any subset of $\mathcal{X}$ containing $y$ .

In most of our examples and applications $\mathcal{X}$ will be equal to $\mathbb{R}$ , $\mathbb{R}^+$ , or $\mathbb{R}^n$ but in some cases we consider majorization over an interval or, more generally, a convex subset of $\mathbb{R}^n.$ If we do not explicitly mention the set on which $g$ majorizes $f$ , then we implicitly mean the whole domain of $f$ . But we'll try to be as explicit as possible, because our treatment, unlike some earlier ones, does not just discuss majorization over the whole space where $f$ is defined.

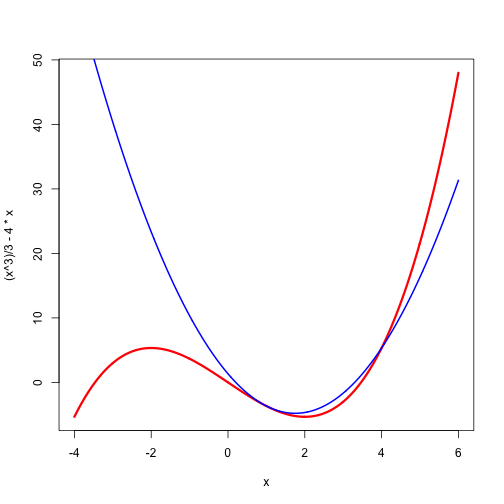
As an example, consider the cubic $f:x\rightarrow\frac13 x^3-4x$ which is majorized at $+1$ on the half-open interval $(-\infty,4]$ by the quadratic $g: x\rightarrow\frac43-7x+2x^2$ . This particular quadratic is constructed, by the way, by solving the equations $f(1)=g(1), f'(1)=g'(1),$ and $f(4)=g(4)$ . On the other hand it is easy to see that a non-trivial cubic $f$ cannot be majorized at any $y$ by a quadratic $g$ on the whole real line, because $g-f$ , which is again a non-trivial cubic, would have to be non-negative for all $x,$ which is impossible.

Figure 2: Quadratic Majorizer of a Cubic on an Interval

It follows directly from the definition that $g$ majorizes $f$ at $y$ if and only if $g-f$ has a global minimum over $\mathcal{X}$ , equal to zero, at $y$ . And majorization is strict if this minimum is unique. Thus a necessary and sufficient condition for majorization at $y\in\mathcal{X}$ is $\min_{x\in\mathcal{X}}\ (g(x)-f(x))=g(y)-f(y)=0.$ Since a global minimum is also a local minimum, it follows that if $g$ majorizes $f$ at $y\in\mathcal{X}$ then $g-f$ has a local minimum , equal to zero, over $\mathcal{X}$ at $y$ . This is a convenient necessary condition for majorization. A sufficient condition for $g$ to majorize $f$ at $y$ is that $g-f$ is a convex function with a minimum at $y$ equal to zero. Because of convexity this minimum is then necessarily the global minimum.

If $g$ majorizes $f$ at $y\in\mathcal{X}$ then the points $y\in\mathcal{X}$ where $g(y)=f(y)$ are called support points. If majorization is strict there is only one support point. There can, however, be arbitrarily many.

Consider $f:x\rightarrow x^2-10\sin^2(x)$ and $g:x\rightarrow x^2$ . Then $g$ majorizes $f$ on the real line, with support points at all integer multiples of $\pi$ . This is illustrated in Figure 3.

Figure 3: Quadratic Majorizer with an Infinite Number of Support Points

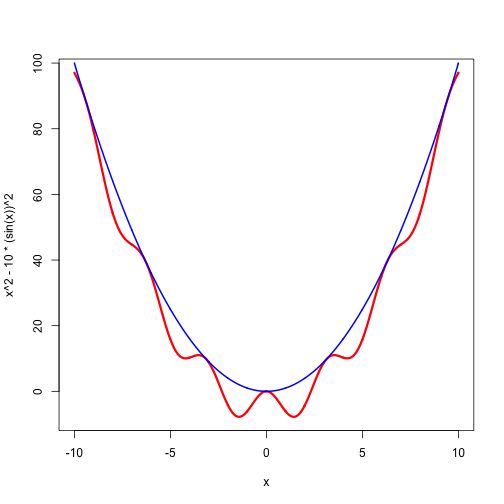
In fact if $f:x\rightarrow\max(x,0)$ and $g:x\rightarrow|x|$ then $g$ majorizes $f$ at all $y\leq 0$ , and thus there even is a continuum of support points. And actually $f$ itself majorizes $f$ at all $y\in\mathcal{X}.$