The Reciprocal | Block Relaxation Algorithms in Statistics -- Part II

II.1.5.1: The Reciprocal

Minimizing the function $f(x)=ax-\log(x)$ , where $a$ > $0$ is a constant, over $x$ > $0$ is trivial. The first and second derivatives of $f$ are $f'(x)=a-\frac{1}{x},$ and $f''(x)=\frac{1}{x^2}.$ We see from $f''(x)>0$ that $f$ is strictly convex on the positive reals. It has its unique minimum for $a-1/x=0$ , i.e. for $x=1/a$ , and the minimum value is $1+\log(a)$ .

Thus iterative algorithms to minimize the function, which can also be thought of as iterative algorithms to compute the reciprocal of a positive number $a$ , are of little interest in themselves. But it is of some interest to compare various algorithms, such as different majorization methods, in terms of robustness, speed of convergence, and so on.

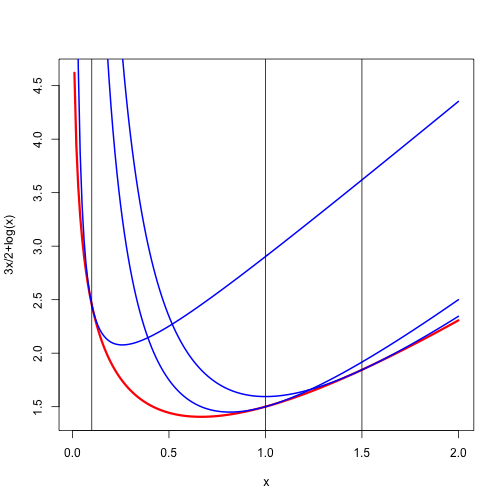
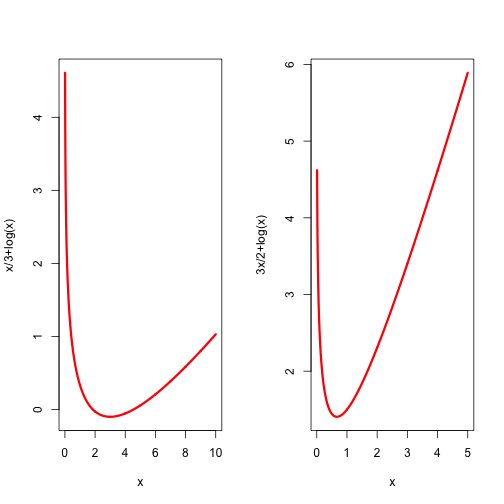
Here are plots of the function $f$ for $a=1/3$ and for $a=3/2$ .

plot of chunk afuncs

Figure 1: ax+log(x) for a = 1/3 (left) and a=3/2 (right)

Because $-\log(x)=\log(1/x)$ the concavity of the logarithm shows that $\log(\frac{1}{x})\leq\log(\frac{1}{y})+y\left(\frac{1}{x}-\frac{1}{y}\right),$ or $-\log(x)\leq-\log(y)+\frac{y}{x}-1.$ Thus $g(x,y)=ax-\log(y)+\frac{y}{x}-1$ majorizes $f$ , and minimizing the majorizer gives the very simple algorithm $x^{(k+1)}= \sqrt{\frac{x^{(k)}}{a}}.$ The derivative of the update function $h(x)\mathop{=}\limits^{\Delta}\sqrt{x/a}$ at $1/a$ is $1/2$ . Thus our majorization iterations have linear convergence, with ratio $1/2$ . If $x^{(0)}<1/a$ the algorithm generates an increasing sequence converging to $1/a$ . If $x^{(0)}>1/a$ we have a decreasing sequence converging to $1/a$ . Because $ax^{(k+1)}=\sqrt{ax^{(k)}}$ we have the explicit expression $x^{(k)}=a^{\left(\frac{1}{2^k}-1\right)}\left(x^{(0)}\right)^{\left(\frac{1}{2^k}\right)}.$

Here we show the majorization for $a=3/2$ and $y$ equal to $1/10, 1$ and $3/2$ .

Figure 2: Majorization of 3x/2+log(x) at y=1/10,1, and 3/2