Dinkelbach Majorization

In S-majorization we make sure the sandwich inequality remains true by requiring that $g(x,y)\leq g(y,y)=f(y)\Rightarrow f(x)\leq g(x,y).$ An alternative requirement, that also leads to a sandwich inequality, is $g(x,y)\leq g(y,y)=f(y)\Rightarrow f(x)\leq f(y),$ or, in iteration terms, If $g(x^{(k+1)},x^{(k)})\leq g(x^{(k)},x^{(k)})$ then $f(x^{(k+1)})\leq f(x^{(k)})$ .

Suppose $f$ is a real-valued function on $\mathcal{X}$ and $g$ is a real-valued function on $\mathcal{X}\otimes\mathcal{X}$ . We say that $g$ Dinkelbach majorizes $f$ on $\mathcal{X}$ if

if $g(x,y)\leq g(y,y)$ then $f(x)\leq f(y)$ for all $x,y\in\mathcal{X}$ ,
$g(y,y)=f(y)$ for all $y\in\mathcal{X}$ .

Dinkelbach Majorization is strict if the first condition can be replaced by

if $g(x,y)<g(y,y)$ then $f(x)<f(y)$ for all $x,y\in\mathcal{X}$ .

The D here stands for Dinkelbach, who proposed a forerunner of D majorization in a classic fractional programming article [Dinkelbach [1967]]. In S-majorization we require that $g$ majorizes $f$ on the sublevel set $\mathcal{L}(y)=\{x\in\mathcal{X}\mid g(x,y)\leq g(y,y)\}.$ In D-majorization we require that $f$ attains its maximum on the sublevel set $\mathcal{L}(y)$ at $y$ .

Suppose $f$ is a fractional function of the form $f(x)=\frac{a(x)}{b(x)},$ with $b(x)>0$ for $x\in\mathcal{X}$ . Then $g(x,y)=f(y)+a(x)-f(y)b(x)$ D-majorizes $f$ on $\mathcal{X}$ .

Clearly $g(y,y)=f(y)+a(y)-\frac{a(y)}{b(y)}b(y)=f(y).$ Moreover $g(x,y)\leq g(y,y)$ can be written as $f(y)+a(x)-f(y)b(x)\leq f(y)$ which implies $f(x)\leq f(y)$ .

Suppose $g(x,y)=f(y)+f'(y)(x-y)+\frac12 a(x-y)^2,$ with $a>0$ . Now $g(x,y)\leq f(y)$ if and only if $(x-y)(f'(y)+\frac12a(x-y))\leq 0,$ Or $x$ must be in the interval between $y$ and $y-\frac{2f'(y)}{a}$ . For a cubic $f(x)=f(y)+f'(y)(x-y)+\frac12 f''(y)(x-y)^2+\frac16 f'''(x-y)^3$ we require that $(x-y)(f'(y)+\frac12 f''(y)(x-y)+\frac16 f'''(x-y)^2)\leq 0$ for all $x$ in the interval between $y$ and $y-\frac{2f'(y)}{a}$ .

Suppose $f$ is increasing and differentiable. We have $f'(y)\geq 0$ for all $y$ . Thus for any $x\in[y-\frac{2f'(y)}{a},y]$ we have $x\leq y$ and consequently $f(x)\leq f(y)$ . In other words: an increasing function is Dinkelbach majorized by any convex quadratic.

Consider $f$ with $f(x)=\frac14 x^4$ and let us majorize at $y=1$ by a convex quadratic $g$ which has both $g(1)=f(1)=\frac14$ and $g'(1)=f'(1)=1.$ It follows that $g(x)=ax^2+(1-2a)x+(a-\frac34)$ for some $a\geq 0$ . Note that if we would also require that $g''(1)\geq h''(1)$ then we need $a\geq\frac32.$

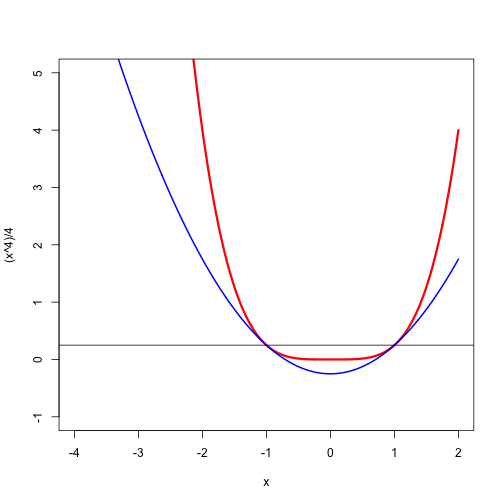
If we compute $h=g-f$ we find $h(x)=-\frac14(x-1)^2(x^2+2x+(3-4a)).$ Majorization at $y$ would mean $h(x)\geq 0$ for all $x$ , which is clearly impossible because $h(x)$ will be negative for $x$ very large and $x$ very small.

We have $h(x)\geq 0$ if and only if $q(x)\mathop{=}\limits^{\Delta}x^2+2x+(3-4a)\leq 0$ .The quadratic $q$ can only be non-positive if it has two real roots, which happens if $a\geq\frac12$ , and then $q$ is non-positive between its two real roots, which are $-1-\sqrt{4a-2}$ and $-1+\sqrt{4a-2}.$

The sublevel set $\mathcal{L}(1)=\{x\mid g(x)\leq\frac14\}$ is the interval $[\frac{a-1}{a},1]$ . For S-majorization we need $h(x)\geq 0$ for all $x\in\mathcal{L}(1)$ , which means that interval $[\frac{a-1}{a},1]$ must be a subset of interval $[-1-\sqrt{4a-2},-1+\sqrt{4a-2}].$ Thus we must have $1\leq -1+\sqrt{4a-2}$ as well as $\frac{a-1}{a}\geq -1-\sqrt{4a-2}.$ The first inequality gives $a\geq\frac32$ , the second one $a\geq\frac12$ . Thus we have S-majorization at $y=1$ if and only if $a\geq\frac32$ . Figure 1 shows the S-majorization with $a=3/2$ , first globally, and then in closeup with $\mathcal{L}(1)=[\frac13,1]$ on the horizontal axis. Note that the S-majorizer is certainly not a majorizer. Also note that $a=3/2$ actually makes $g''(1)=f''(1)$ , which means the quadratic S-majorizer is the quadratic approximation used in Newton's method.

Figure 1: S-majorization at y = 1 for a = 1.5.

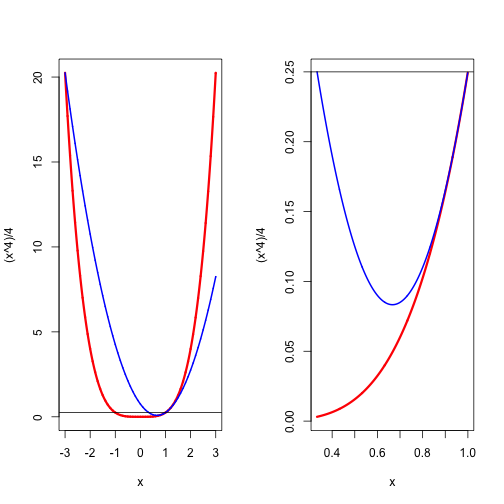
For D-majorization we need $f(x)\leq f(1)=\frac14$ for all $x\in\mathcal{L}(1)$ which is the case if $\frac{a-1}{a}\geq -1$ , i.e. $g$ D-majorizes $f$ at $y=1$ if and only if $a\geq\frac12.$ In figure 2 we see that a D-majorizer can actually be a minorizer ! Of course the S-majorization in figure 1 is also a D-majorization.

Figure 2: D-majorization at y = 1 for a = 0.5.