Comparing Majorizations

The set of all real-valued functions $\mathcal{M}_Y(f)$ that majorize $\ f$ on $\mathcal{Y}$ is convex.

If we order $\mathcal{M}_Y(f)$ by $g\leq_Y h$ if $g(y)\leq h(y)$ for all $y\in\mathcal{Y}$ , then $\langle\mathcal{M}_Y(f),\leq_Y\rangle$ is a lattice, because if $g$ and $h$ majorize $\ f$ on $\mathcal{Y}$ , then so do the pointwise maximum and minimum of $g$ and $h.$

In fact the lattice $\langle\mathcal{M}_Y(f),\leq_Y\rangle$ is inf-complete, because the pointwise infimum of a set of majorizing functions again majorizes. Clearly $f$ itself is the minimal element of the lattice. The lattice is not sup-complete, although it is if we consider the set of extended real valued functions which can take the value $+\infty$ .

The following needs to be repaired -- only true for majorization at a point 03/28/15

Note, however, that the pointwise maximum of a finite number of majorizing functions does majorize. If $f(x)\leq g_i(x,y)$ and $f(x)=g_i(x,x)$ for all $i=1,\cdots,n$ then $f(x)=\max_{i=1}^n g_i(x,x)$ and $f(x)\leq\max_{i=1}^n g_i(x,y)$ . But if $\mathcal{I}$ is infinite, then $\sup_{i\in\mathcal{I}}g_i(x,y)$ can be infinite as well, and in that case it is not a majorization function. In contrast it is always true that $f(x)\leq\inf_{i\in I}g_i(x,y)$ .

We can actually give an even stronger result than inf-completeness. Suppose $g_i(x,y_i)-f(x)\geq 0$ for all $i=1,\cdots,n$ and for all $x\in\mathcal{X}$ , and $g_i(y_i,y_i)-f(y_i)=0$ for all $i=1,\cdots,n$ . Thus $g_i$ majorizes $f$ at $y_i$ . Now let $h(x)=\min_{i=1}^n\ (g_i(x,y_i)-f(x))$ then $h(x)\geq 0$ for all $x\in\mathcal{X}$ and $h(y_i)=0$ for all $i=1,\cdots,n$ . Thus $f(x)+h(x)=\min_{i=1}^n g_i(x,y_i)$ majorizes $f$ at $y_1,\cdots,y_n$ .

As an example, consider the function $f:x\rightarrow x^4$ on $[-1,+1]$ . On that interval we have $f''(x)\leq 12$ and thus if $-1\leq y\leq +1$ we have the quadratic majorizer $g(x,y)=y^4+4y^3(x-y)+6(x-y)^2.$ Now take the $y_i$ to be the 11 points $-1.0,-0.8,\cdots,0.8,1.0$ and take $h(x)$ to be the minimum of the $g(x,y_i)$ .

Figure 1: Piecewise Quadratic Majorization at Multiple Points of a Quartic

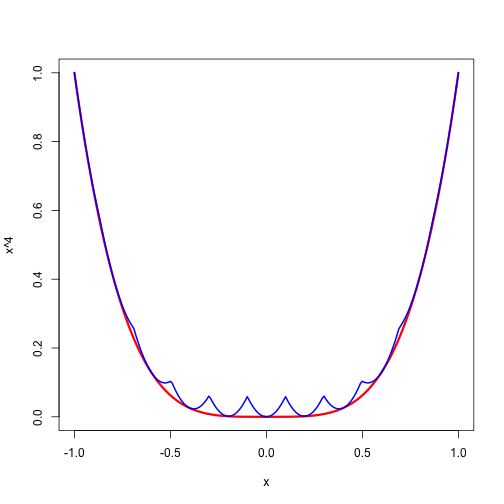
Of course $\min_{-1\leq y\leq +1} g(x,y)=f(x)$ which means we can make the majorization as sharp as we want by increasing the number of support points.